Часто нам приходится делать выбор в условиях, когда вознаграждение от альтернатив представляет собой распределение, а не фиксированную величину. Профессор Скотт Пейдж уверен: здесь пригодятся модели — математические формулы и диаграммы, помогающие понять этот мир. Об этом его книга. Давайте посмотрим, как всё работает.
Задачи о многоруком бандите
Модельное мышление
Воспользуемся таким классом моделей, как задачи о многоруком бандите. Они применимы к широкому спектру реальных ситуаций. Любой выбор из совокупности действий, обеспечивающий неопределенный выигрыш, — испытания лекарственных препаратов, выбор площадки для размещения рекламы, выбор технологий, решение об использовании ноутбуков на занятиях— можно смоделировать в виде такой задачи.
Человек, которому нужно решить такую задачу, должен поэкспериментировать с альтернативами, чтобы определить распределение выигрышей. Эта особенность задач о многоруком бандите создает компромисс между использованием (поиском наилучшей альтернативы) и исследованием (выбором альтернативы, которая на данный момент показала лучшие результаты).
Давайте разберем особый класс задач о многоруком бандите по Бернулли, а затем опишем общую модель.
По Бернулли
Начнем с подкласса задач о многоруком бандите, в которых каждая альтернатива имеет фиксированную вероятность обеспечения успешного исхода. Их еще называют частотными задачами, поскольку ответственный за принятие решений ничего не знает о распределениях и получает информацию о них по мере исследования альтернатив.
Заглянуть на страничку акции
Вот пример. Предположим, у компании по чистке дымоходов есть список телефонных номеров недавних покупателей домов. Сотрудники тестируют три способа сделать коммерческое предложение:
- запланированная встреча («Здравствуйте! Я звоню, чтобы договориться о времени ежегодной чистки вашего дымохода»),
- выражение обеспокоенности («Здравствуйте! Знаете ли вы, что грязный дымоход может стать причиной пожара?»),
- индивидуальный подход («Здравствуйте! Меня зовут Хилди. Мы с отцом основали компанию по чистке дымоходов четырнадцать лет назад»).
Каждое коммерческое предложение имеет неизвестную вероятность успеха. Предположим, компания сначала пробует подход «запланированная встреча» и терпит неудачу. Тогда она переходит ко второму подходу — выражению обеспокоенности — и заполучает клиента. Подход срабатывает и во время следующего звонка, но еще после трех звонков тоже терпит неудачу. Компания применяет третий подход, который срабатывает во время первого звонка и терпит неудачу в ходе следующих четырех. После десяти звонков второй подход обеспечивает самый высокий процент успеха, однако первый подход применялся только один раз.
Человек, принимающий решение, становится перед выбором между использованием (выбором наиболее подходящей альтернативы) и исследованием (возвратом к двум другим альтернативам для получения дополнительной информации).
Алгоритмы
Для более глубокого понимания компромисса между исследованием и использованием сравним два эвристических алгоритма.
1. «Выборочное исследование, затем жадный выбор». Подразумевает проверку альтернатив фиксированное количество раз M, после чего следует выбор альтернативы с максимальным средним выигрышем. Для того чтобы определить величину M, можно воспользоваться урной Бернулли и правилами квадратного корня. Стандартное отклонение среднего соотношения ограничено сверху величиной 
. Если каждая альтернатива тестируется 100 раз, стандартное отклонение среднего соотношения будет равно 5 процентам. Если применить правило двух стандартных отклонений для выявления значимого различия, можно уверенно провести разграничение между соотношениями, отличающимися на 10%. Если одна альтернатива обеспечивает успешный исход в 70% случаев, а другая — в 55% случаев, мы можем с 95% уверенности утверждать, что первый вариант лучше.
2. «Эвристический алгоритм адаптивного уровня исследования». Выделяет по десять исходных испытаний на каждую альтернативу. Следующие двадцать испытаний распределяются пропорционально доле успешных попыток. Если во время первых десяти испытаний одна альтернатива обеспечивает шесть успешных попыток, а другая только две, то первая альтернатива получит три четверти от следующих двадцати испытаний. Вторая группа из двадцати испытаний тоже может быть распределена в соответствии с отношением квадратов вероятностей успеха. Если успешные попытки продолжатся в тех же пропорциях, лучшая альтернатива получит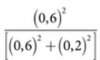 
или 90% третьей группы из двадцати испытаний. В каждой последующей группе из двадцати испытаний можно с определенной скоростью увеличивать показатели степени вероятностей. Увеличивая с течением времени темпы использования, второй алгоритм улучшает первый. Если у одной альтернативы намного выше вероятность успеха по сравнению с другой альтернативой, скажем 80% против 10 процентов, алгоритм не станет тратить сотню испытаний на вторую альтернативу. Однако если обе вероятности имеют близкие значения, алгоритм продолжит экспериментировать.
Следование эвристическому алгоритму «выборочное исследование, а затем жадный выбор» не только неэффективно, но порой даже неэтично. Когда Роберт Бартлетт испытывал искусственное легкое, процент его успеха существенно превышал показатель других альтернатив. Продолжение их тестирования, тогда как искусственное легкое демонстрировало наилучшие результаты, привело бы к бессмысленным смертельным исходам. Бартлетт прекратил эксперименты с другими альтернативами. Все пациенты получили искусственное легкое.
Байесовские задачи
Автор книги уверен: важно применять многомодельный подход. То есть смотреть на проблему с нескольких точек зрения. Поэтому попробуем найти лучшую альтернативу еще одним способом.
В байесовской задаче о многоруком бандите у человека, принимающего решение, есть априорные убеждения в отношении распределения вознаграждений от альтернатив. С их учетом он может количественно оценить компромисс между исследованием и использованием, а также (теоретически) принимать оптимальные решения в каждом периоде.
За исключением самых простых задач о многоруком бандите определение оптимального действия требует довольно сложных вычислений. Оно происходит в четыре этапа. Во-первых, мы вычисляем ожидаемое немедленное вознаграждение от каждой альтернативы. Во-вторых, обновляем по каждой альтернативе убеждения в отношении распределения вознаграждений. В-третьих, на основании новых убеждений определяем наилучшие возможные действия во всех последующих периодах с учетом известной информации. И наконец, прибавляем ожидаемое вознаграждение от действия в следующем периоде к ожидаемым вознаграждениям от оптимальных будущих действий. Эта сумма известна как индекс Гиттинса.
В каждом периоде оптимальное действие имеет максимальный индекс Гиттинса. Обратите внимание, что вычисление индекса дает количественную оценку значимости исследования. При испытании той или иной альтернативы индекс Гиттинса не равен ожидаемому вознаграждению. Он равен сумме всех будущих вознаграждений при условии совершения нами оптимальных действий с учетом полученной информации.
Вычислить индекс Гиттинса довольно сложно. В качестве примера предположим, что существует надежная альтернатива, которая гарантированно обеспечит прибыль в 500 долларов, и рискованная альтернатива, которая с вероятностью 10% всегда приносит 1000 долларов, а в оставшихся 90% случаев не дает никакой прибыли. Для того чтобы вычислить индекс Гиттинса для рискованной альтернативы, сперва зададимся вопросом, что может происходить: либо она всегда дает прибыль 1000 долларов, либо не дает никакой прибыли. А затем проанализируем, как каждый исход влияет на наши убеждения. Если бы мы узнали, что рискованная альтернатива принесет 1000 долларов, мы бы всегда выбирали ее. Если бы нам стало известно, что она не принесет никакой прибыли, в будущем мы всегда выбирали бы надежную альтернативу. Таким образом, индекс Гиттинса по рискованной альтернативе соответствует 10% вероятности вознаграждения в размере 1000 долларов в каждом периоде и 90% вероятности вознаграждения в размере 500 долларов в каждом периоде, за исключением первого. В ситуации многократного выбора альтернативы это дает в среднем около 550 долларов за каждый период. Отсюда следует, что рискованная альтернатива — лучший выбор.
При принятии важных решений в области бизнеса, политики и медицины, где данные собирать легче, модели многорукого бандита применяются очень широко. Компании, творцы политики и некоммерческие организации экспериментируют с альтернативами, а затем используют наиболее результативные из них. Вы тоже так можете.
Чтобы лучше разобраться в теме, загляните в книгу «Модельное мышление»
Обложка поста — unsplash.com
