Риску подвержена вся наша жизнь. Начиная с открытия шампанского на Новый год и заканчивая деловой сделкой. В некоторых случаях вы можете снизить негативные последствия риска, разделив его с партнером. С шампанским такое вряд ли удастся провернуть, тогда как в рабочих моментах об этом стоит как минимум задуматься. В книге «Стратегические игры» приводится алгоритм рассуждений, к которому стоит прибегнуть при разделении риска.
Пример с фермерами
Сначала проанализируем возможность взаимовыгодного разделения риска. Предположим, ваш приятель сталкивается с аналогичным риском, но в то время, когда у вас плохая погода, на его ферме погода хорошая и наоборот. (Допустим, вы живете на противоположных концах острова и дождевые облака приходят либо на одну, либо на другую его сторону, но не на обе сразу.)
Корреляция — это зависимость между двумя любыми неопределенными величинами (в данном примере между риском одного фермера и риском другого). Следовательно, можно сказать, что между риском вашего приятеля и вашим риском существует полная отрицательная корреляция. Ваш с приятелем совокупный доход составляет 200 000 долларов, какой бы ни была погода, то есть он совершенно безрисковый.

Ваши риски зависят от погоды. Источник
Вы можете заключить между собой контракт, по условиям которого каждый из вас получит гарантированных 100 000 долларов: вы обещаете выплачивать приятелю 60 000 долларов в те годы, когда вам сопутствует удача, а он — в те годы, когда ему сопутствует удача. Объединив свои риски, вы их устраняете.
Пример из реальной жизни
Валютные свопы — еще один показательный пример отрицательной корреляции рисков в реальной жизни. Американская компания, экспортирующая продукцию в Европу, получает доход в евро, но ее интересует прибыль в долларах, зависящая от колебаний обменного курса евро—доллар. Со своей стороны, европейская компания, экспортирующая продукцию в США, сталкивается с аналогичной неопределенностью в отношении прибыли, выраженной в евро. Когда курс евро по отношению к доллару падает, доход американской компании в евро составляет меньшую сумму в долларах, а долларовый доход европейской компании — более крупную сумму в евро. Когда курс евро по отношению к доллару повышается, складывается противоположная ситуация. Таким образом, колебания обменного курса создают отрицательно коррелированные риски для обеих компаний. Следовательно, обе могут их снизить, заключив контракт о соответствующем обмене доходами.
Даже при отсутствии отрицательной корреляции разделение рисков имеет свои преимущества. Вернемся к вашей роли фермера и допустим, что вы с приятелем сталкиваетесь с рисками, не зависящими друг от друга, как если бы тучи подбрасывали монету, чтобы решить, на какую сторону острова отправиться. В таком случае существуют четыре возможных исхода, каждый с вероятностью 1/4. Ваш с приятелем доход при этих четырех исходах представлен в левой части таблицы.
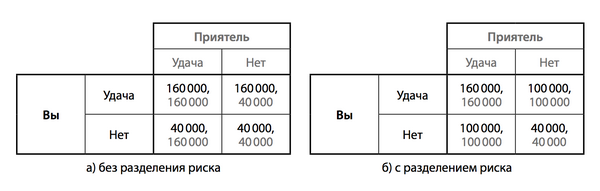
Но предположим, вы должны заключить контракт о разделении риска поровну; тогда ваш доход будет отображен в правой части таблицы. Ваш средний (ожидаемый) доход в каждой таблице составляет 100000 долларов, однако без договора о разделении риска каждый из вас получил бы 160 000 долларов, или 40 000 долларов с вероятностью 1/2 каждый. При наличии контракта вы оба получили бы по 160 000 долларов с вероятностью 1/4, по 100 000 долларов с вероятностью 1/2 и 40 000 долларов с вероятностью 1/4. Таким образом, контракт о разделении риска позволяет каждому из вас снизить вероятность двух крайних исходов с 1/2 до 1/4 и повысить вероятность среднего исхода с 0 до 1/2. Иными словами, контракт уменьшил риск каждого из вас.
Политика страховых компаний в отношении риска
В действительности вы с приятелем можете уменьшать свои риски посредством их разделения при условии, что между вашими доходами нет полной положительной корреляции (то есть до тех пор, пока удача не улыбнется вам обоим). А группе более двух человек, риски которых в определенной мере независимы друг от друга, закон больших чисел позволяет еще сильнее снизить риск каждого участника. Именно так и поступают страховые компании: объединив подобные, но независимые риски многих людей, они могут выплатить страховое возмещение каждому, кто понесет существенные убытки. Этот же принцип лежит в основе диверсификации инвестиционного портфеля: вкладывая средства во много разных активов с разными типами и степенями риска, вы тем самым уменьшаете общий уровень подверженности риску.

Страховые компании объединяют подобные, но независимые риски. Источник
Однако такие механизмы разделения рисков зависят от публичной наблюдаемости результатов и возможности контролировать выполнение условий контракта. В противном случае у каждого фермера возникает соблазн сделать вид, что ему не повезло, или просто нарушить условия договора о разделении риска, когда ему сопутствует удача. Точно так же страховая компания может безо всяких оснований отказать в выплате страхового возмещения, но желание сохранить репутацию может удержать ее от этого шага.
По материалам книги «Стратегические игры»
Обложка поста: pixabay.com







